
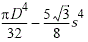
Because r is the distance to the axis of rotation from each piece of mass that makes up the object, the moment of inertia for any object depends on the chosen axis. We defined the moment of inertia I of an object to be I = ∑ i m i r i 2 I = ∑ i m i r i 2 for all the point masses that make up the object. This section is very useful for seeing how to apply a general equation to complex objects (a skill that is critical for more advanced physics and engineering courses).
In this section, we show how to calculate the moment of inertia for several standard types of objects, as well as how to use known moments of inertia to find the moment of inertia for a shifted axis or for a compound object. In the preceding section, we defined the moment of inertia but did not show how to calculate it.

By the end of this section, you will be able to:


 0 kommentar(er)
0 kommentar(er)
